- A
- B
- C
- D
- E
- F
- G
- H
- I
- J
- K
- L
- M
- N
- O
- P
- Q
- R
- S
- T
- U
- V
- W
- X
- Y
- Z
- AA
- AB
- AC
- AD
- AE
- AF
- AG
- AH
- AI
- AJ
- AK
- AL
- AM
- AN
- AO
- AP
- AQ
小明的霍夫曼树 3147
Time Limit: 1 s
Memory Limit: 256 MB
Submission:2
AC:2
Score:0
Description
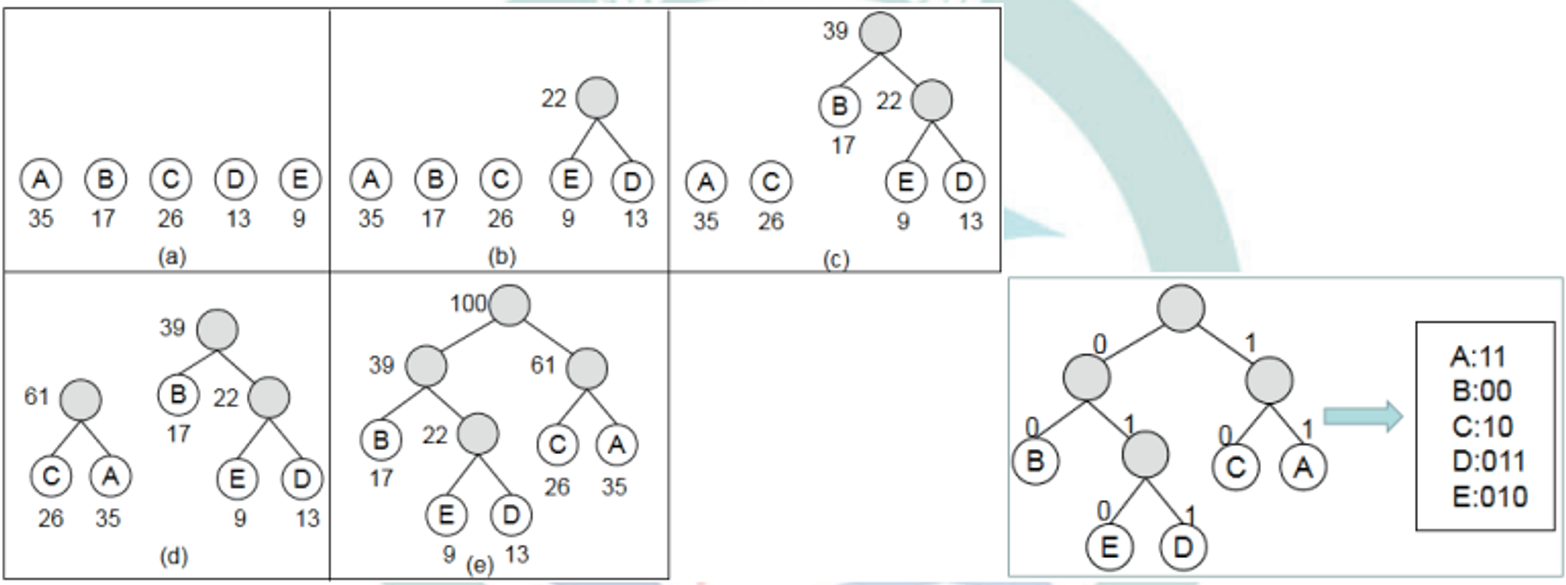
通信中,为了避免歧义,每个字符的二进制编码的前缀互不相同,且用不等长的编码来缩小二进制串的总长度以提高效率。小明在学习了霍夫曼算法后想到了可以用霍夫曼树来求出每个字符的最佳码长,下面是霍夫曼树的实现描述:
1. 初始化:由给定的n个权值构造1棵只有一个根节点的二叉树,得到一个二叉树集合。
2. 选取与合并:从二叉树集合中选取根节点权值 最小的两棵二叉树。其中权值较小的作为左分支,较大的作为右分支,再以两棵树根节点的权值之和作为新根节点,构造出一颗新的二叉树。
3. 删除与加入:从集合中删除作为左、右子树的两棵二叉树,并将新建立的二叉树加入到集合中。
4. 重复 2、3 步,当集合中只剩下一棵二叉树时,这棵二叉树就是霍夫曼树。
有了上述描述,小明认为你已经对这个问题有了就一定了解,所以给你了一个字符串,以每个字母出现的频率作为权值,求出每个字母对应的最佳二进制串是多少?(若频率相同则比较字典序)
Input
一行字符串,长度不超过10000,保证全部为小写英文字母
Output
每个字母以及对应二进制编码串,保证答案唯一
Samples
input
abbcccc
output
a:00
b:01
c:1
Hint