搬砖的JoneySun
Time Limit: 2 s
Memory Limit: 256 MB
Submission:55
AC:22
Score:100.00
Description
JoneySun欧皇附体一发入魂,成功消灭了wifepie逃出了监狱。他回到了家中继续自己的搬砖生活。因为成功消灭了邪恶的wifepie,村长BambooCertain决定给他加个buff,每当JoneySun去到一个地点搬砖,BambooCertain就会通过一些手段给改变JoneySun搬的砖的数量,当然每个地点的砖的数量不一定是一样的,JoneySun每天搬砖的地点也是不一样的。
- 对于点$x$,查询除$x$外所有点的点权与$x$到该点路径上距离$x$点最近的边的边权的异或值之和
Input
第一行一个整数$n(1\le n \le 10^5)$表示树上点的数量
接下来$n-1$行每行$3$个整数$u,v,w,(1\le u ,v \le n,1\le w \lt 2^{20})$表示树上每条边及边权
每个结点的初始点权为$0$
接下来一行一个整数$m$表示$m$次操作
接下来$m$行每行第一个数字$opt$表示操作类型
- $opt=1$接下来两个整数$x,(1\le x \le n),y(1\le y \lt 2^{20})$表示将$x$点的权值修改为$y$
- $opt=2$接下来一个整数$x$,表示查询除$x$外所有点的点权与$x$到该点路径上距离$x$点最近的边的边权的异或值之和
Output
对于每个操作$2$,输出一个整数表示答案
Samples
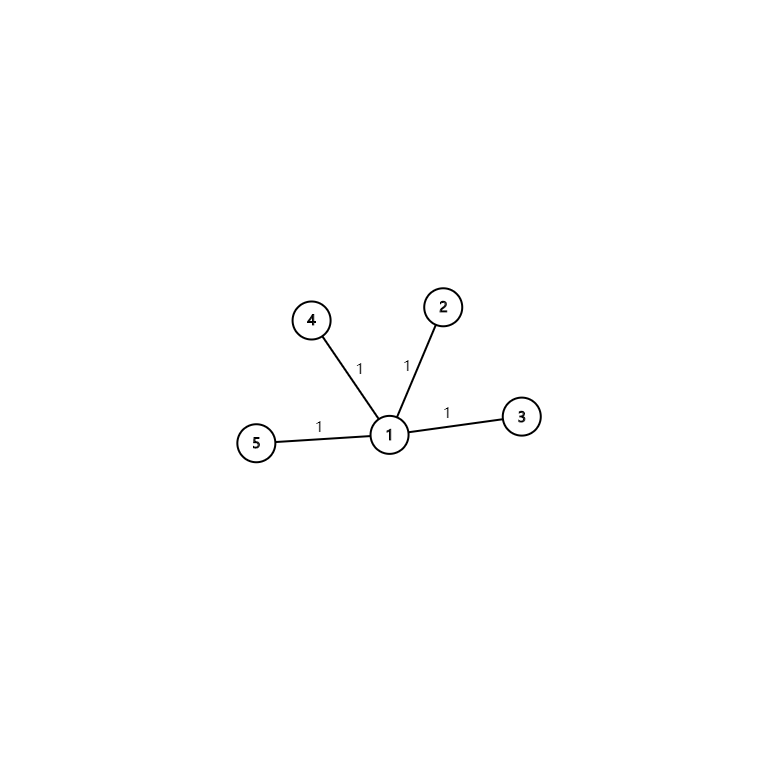
input
5
2 1 1
3 1 1
4 1 1
5 1 1
5
1 2 1
1 1 4
2 1
1 5 1
2 1
output
3
2
Hint