与班尼特·胡迪一起攻克难关
Time Limit: 1 s
Memory Limit: 256 MB
Submission:699
AC:307
Score:85.12
Description
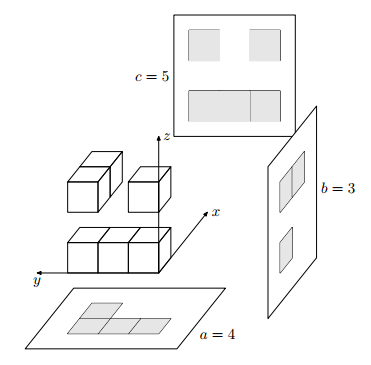
班尼特·胡迪是一位优秀的物理学家,他因发明反重力容器而获2333年诺贝尔物理学奖。他发明的反重力容器是一个封闭的三维立方体,在里面的物品可以不受重力影响。一天,班尼特·胡迪往反重力容器内放入了n个单位立方体,单位立方体的坐标由三个数x,y,z表示,代表这个单位立方体占据着[x, x + 1] × [y, y + 1] × [z, z + 1]的空间。他希望能知道这些单位立方体分别在XoY,XoZ,YoZ平面上的投影面积a,b,c,但他发现他的反重力容器是不透明的,所以他不能通过肉眼观察来确定单位立方体在三个面上的投影面积。聪明的你能帮他一起攻克难关吗?
Input
输入包括多组数据
每组数据的第一行为正整数n,代表班尼特·胡迪放入的单位立方体数目。
接下来有n行数据,每行数据包括三个正整数x, y, z,代表各个单位立方体的坐标。
题目保证输入的单位立方体不重合。
数据范围(1 <= n <= 12, 0 <= x, y, z < 10)
Output
对于每组数据,输出单位立方体在XoY,XoZ,YoZ平面上的投影面积a,b,c
Samples
input
6
0 0 0
0 1 0
0 2 0
0 2 2
1 2 2
0 0 2
output
4 3 5
input
12
0 0 0
0 1 0
0 2 0
0 3 0
1 0 0
1 1 0
1 2 0
1 3 0
2 0 0
2 1 0
2 2 0
2 3 0
output
12 3 4
Hint
x,y,z不一定小于n