和谐 2540
Description
你玩过黑白棋(Reversi or Othello)吗?它在西方和日本很流行。游戏通过相互翻转对方的棋子,最后以棋盘上谁的棋子多来判断胜负。黑白棋的每颗棋子由黑白两色组成,一面白,一面黑。每次落子,把本方颜色的棋子放在棋盘的空格上,若在横、竖、斜八个方向的任一方向上有本方棋子,则被夹在中间的对手棋子全部翻转为本方棋子颜色(且必须存在能够翻转的棋子,才表示当前空格是可以落下的);棋局结束时,以棋子数目来计算胜负,棋子多的一方获胜。在棋盘还没……(节省页面大小省略n字,因为这并没有什么用)。
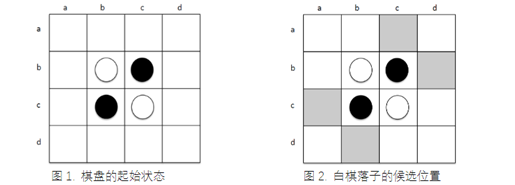
但是我保证接下来你将会看到一款,你从没玩过的全新版本!
这一天,小白和小黑两人因C语言是不是全世界最好的语言起了争执。但是为了建设和谐的社会主义社会,两人理智地打算对弈一局。为了使得对局更加具有趣味性和随机性,两人制定了一系列特殊的规则。
起始时,他们两人各拥有一个属于自己的初始字符串initS(字符串中只可能包含大写的H、Z、N、U)串的长度大于0小于1000。接下来围绕着对弈将有一系列的操作会使他们的串改变,改变的规则如下:
每次当一名棋手落子之前,他们两人会先统计一遍棋盘上所有棋子的总数,记总数为sum。若此时落下的是白子,则将这时黑子的减少数量记为num;反之,若此时落下的是黑子,则将这时白子的减少数量记为num。
我们记一个操作为OP,OP=(num+sum) % 4。但是由于两人对黑白棋的规则不是很理解,所以这一步棋有可能是非法的(非法棋,表示当前棋子落下时,不会有任何其他棋子的颜色被改变,直接将棋权交给对手,且这颗棋子不会落在棋盘上),此时记OP为负无穷。当:
OP=0时,这一步棋会为棋手的串末尾加上一个大写的H字符。
OP=1时,这一步棋会为棋手的串末尾加上一个大写的Z字符。
OP=2时,这一步棋会为棋手的串末尾加上一个大写的N字符。
OP=3时,这一步棋会为棋手的串末尾加上一个大写的U字符。
OP=负无穷时,棋手的串会被整个的反转。
由于两人谁也不想输掉比赛,所以他们随时会趁对方不注意而做一些“小手脚”,他们在自己下完棋子之后(或者无效步数之后),如果发现自己的串中存在连续的“HZNU”字符,那么他们会悄悄的把这串连续的“HZNU”移到串首位置,直到字符串中所有的HZNU都被移动到串首(组合成的HZNU也要被移动)。
(如“ZZZHZNUZZZHZNUZZZ”,会被移动为“HZNUHZNUZZZZZZZZZ”)。
最后给定的Q步操作之后,将两人的串合并,小白的串在前,小黑的串在后,得到最后的这个串称为“总串“。
对上面的规则两人都非常满意,那么该如何判定两人的输赢呢。首先两人会在游戏开始之前各自选出几个字符作为自己的”得分字符“,并共同确认一个”幸运分数“LuckyNumber。
他们会依次取出总串素数位置上的字符,如果该字符是某人选择的“得分字符“,那么该选手就会获得1分。最后谁的得分最接近幸运分数谁就能获得胜利。如果两人打成平局,那么你应该输出”Lucky!”
(例如一开始两人选择4作为幸运分数,小白选择的得分字符为“H、Z”,小黑选择的得分字符为”N、U”,此时若总串为HZNUHZNUHZNU。那么被取出的字符就分别是“ZNHNN”,此时小白的得分是2,小黑的得分是3,小黑的得分更接近幸运分数4,小黑获胜)。
(游戏默认小白先手下棋!数据保证棋盘合理)
Input
每个测试点的输入是单组的。
第一行会给出棋盘的限定大小n行m列(0 < n, m < 100)。接下来的n行将会给出棋盘的初始状态,每行有m个元素,数字0表示棋盘上这个位置有一颗白子,1表示棋盘上这个位置有一颗黑子,字符“#” 表示棋盘上这个位置空缺。棋盘的左上角位置记为(1,1).
给定棋盘后,接下来的两行分别给出的是小白和小黑的初始字符串initS。
给定初始字符串后接下来的一行将给出小白的得分字符。首先是一个数字X表示小白选择了X个得分字符,后面给出X个小白选择的得分字符,用空格分开。(0<=X<=4)
接下来的一行将给出小黑的得分字符。首先是一个数字Y表示小黑选择了Y个得分字符,后面给出Y个小黑选择的得分字符,用空格分开。(0<=Y<=4)
接着的一行给出两个数字Q和LuckyNumber,表示接下来两人将要对弈Q手,并且他们确认了幸运数字为LuckyNumber(0<=Q<=100 , -1e5<=LuckyNumber<=1e5 )。
接下来将会有Q行,每行给定两个坐标u,v,表示这一次小白(或者小黑)将要将棋子落在棋盘(u,v)上。数据保证棋子的落点没有 被占用。(0<u<=n ,0<v<=m)
Output
如果小白获得了胜利请输出“C is the best!”;如果小黑获得了胜利请输出“C is not the best!” ;如果平局请输出“Lucky!”
Samples
Hint
注意如下例子,
#####
#####
##0##
###0#
####1
此时(1,1)落子是无效的,因为要保证翻转的棋子中间不能有空格。
----------------------------------------------------------------------------
对于第一组样例的解释,小白在棋盘(2,2)的位置落子之后,棋盘变成
###01
#0001
##1##
#####
#####
此时,sum=6,num=1。op=(sum+num)%4=3。
所以此时给小白的串加上一个U。变成了“HHHHHU”
游戏结束总串为“HHHHHUHZHZH”.
得分字符分别为“H”、“H”、“H”、“H”、“H”。因为小白选择了”H“所以他共得到了5分。小黑得分为0。
幸运数字是5,所以小白的得分更加接近幸运数字,判定小白胜利,输出”C is the best!“
----------------------------------------------------------------------------
对于第二组样例的解释,小白将在(7,5)的位置落子,则棋盘变为:
##########
##########
##########
##########
####000###
####00####
####0#####
##########
##########
##########
此时棋盘上的sum=5,num=1。得出op=(sum+num)%4=2,此时给小白的串加上‘N’,小白的串变为了”HZN“。(注意此时虽然小白将棋盘上所有的棋子变成了白色,但是并不能判小白获胜)。
游戏结束得出了总串为"HZNNNNHZZZNZZ"。
此时得分字符分别为"Z" 、"N"、”N“、”H“、”N“、”Z“。
小白选择了‘N’和‘U’所以共得到3分。
小黑选择了‘H’所以共得到1分。
此时幸运数字为2,两人的分数和幸运数字是一样接近的。所以此时判定为平局。输出”Lucky!“。