踢足球 2779
Description
这一天,小蔡又带着他的足球来到了球场上踢人。已知球场是一个二维平面,经过一番激烈的战斗,小蔡的位置在(X,Y),在她周围有N个敌人,位置分别是(A1,B1)、(A2,B2)...(AN,BN)。现在小蔡同学可以向一个方向踢出足球,足球最远可以踢到距离发射点M个单位的位置,足球攻击到敌人后就会停下,并且这个足球可以分裂出多个新的足球(相当于在这个位置踢出多个新的足球),继续攻击范围内的其他所有敌人。
现在给出小蔡和N个敌人的位置以及足球的射程M,求这N个敌人能否都被踢到。
Input
第一行为两个整数X和Y,代表小蔡的坐标(X,Y);(-100000<=X<=100000,-100000<=Y<=100000)
第二行为一个正整数N,代表敌人的数量;(1<=N<=10)
接下来N行,每行两个整数Ai和Bi,代表敌人的坐标(Ai,Bi);(-100000<= Ai <=100000,-100000<= Bi <=100000)
最后一行为一个正整数M,代表足球的射程。(1<=M<=100000)
所有坐标都不会重复。
Output
如果这N个敌人都能被踢到,就输出“YES”,否则输出“NO”。
Samples
Hint
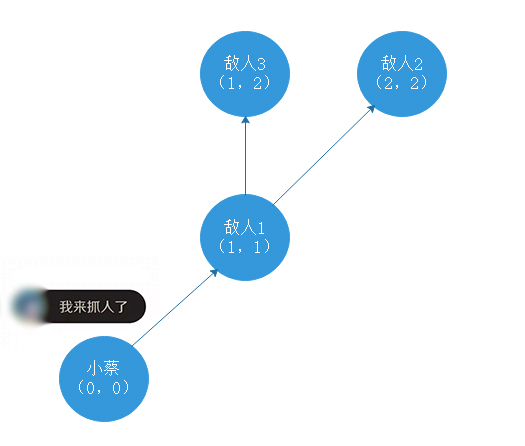
对于样例一,小蔡在(0,0)位置上,因为(0,0)和(1,1)之间的距离小于等于足球射程2,所以他可以先踢到(1,1)位置上的敌人;因为(1,1)和(2,2)之间的距离小于等于足球射程2,并且(1,1)和(1,2)之间的距离小于等于足球射程2,所以足球可以在(1,1)位置上分裂出两个新的足球,其中一个新的足球可以踢到(2,2)位置上的敌人,另一个新的足球可以踢到(1,2)位置上的敌人。所以足球可以踢到所有敌人。足球的运动轨迹如图所示: